Diagramas de Venn

Diagrama que representa conjuntos y muestra gráficamente donde se intersecan esos conjuntos. En él, cada conjunto está representado por la región dentro de una curva cerrada simple. Se nombra así en honor de Venn, un inglés que primero utilizó este tipo de diagrama
Los diagramas de Venn son “ilustraciones usadas en la rama de la matemática conocida como teoría de conjuntos. Estos diagramas se usan para mostrar gráficamente la relación matemática o lógica entre diferentes grupos de cosas (conjuntos), representando cada conjunto mediante un óvalo o círculo”.

Este tipo de diagramas es conocido por muchos pues es comúnmente utilizado en las matemáticas para trabajar en el tema “conjuntos”, tan popular en la escuela primaria. Sin embargo, su aplicación es mucho más amplia y permite al estudiante identificar si existe o no relación entre los elementos de un conjunto y otro(s).

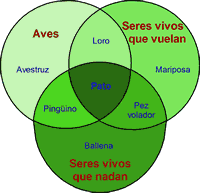
Un Diagrama de Venn de tres conjuntos tiene 7 áreas diferenciadas. En el siguiente ejemplo se comparan tres conjuntos: aves, seres vivos que nadan y seres vivos que vuelan; el diagrama permite visualizar fácilmente los elementos de cada conjunto que comparten propiedades.

-ORIGEN:

Los diagramas de Venn tienen el nombre de su creador, John Venn, matemático y filósofo británico. Estudiante y más tarde profesor del Caius College de la Universidad de Cambridge, Venn desarrolló toda su producción intelectual en ese ámbito.

Los diagramas que hoy conocemos fueron presentados en julio de 1880 en el trabajo titulado De la representación mecánica y diagramática de proposiciones y razonamientos, que tuvo gran repercusión en el mundo de la lógica formal. Los diagramas de Venn tienen varios antecedentes. La primera representación gráfica de deducciones lógicas —y, en particular, de silogismos— se atribuye comúnmente a Gottfried Leibniz. Variantes de la misma fueron empleadas luego por George Boole y Augustus De Morgan, pero fue el gran matemático suizo Leonhard Euler quien primero introdujo una notación clara y sencilla. El siguiente diagrama muestra de otro modo la relación de inclusión del ejemplo dado en la introducción.

-LINKS:

http://es.wikipedia.org/wiki/Diagrama_de_Venn

http://www.mathematicsdictionary.com/spanish/vmd/full/v/venndiagram.htm
http://www.eduteka.org/modulos/4/118/